II. Неравенства с параметрами.

1. Основные определения

Неравенство

f(a, b, c, …, k, x)>j(a, b, c, …, k, x),                  (1)

где a, b, c, …, k – параметры, а  x – действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.

Любая система значений параметров а = а₀, b = b₀, c = c₀, …,  k = k₀, при некоторой функции

f(a, b, c, …, k, x)  и

j(a, b, c, …, k, x

имеют смысл в области действительных чисел, называется системой допустимых значений параметров.

называется допустимым значением х, если

f(a, b, c, …, k, x)  и

j(a, b, c, …, k, x

принимают действительные значения при любой допустимой системе значений параметров.

Множество всех допустимых значений х называется областью определения неравенства (1).

Действительное число х₀ называется частным решением неравенства (1), если неравенство 

f(a, b, c, …, k, x₀)>j(a, b, c, …, k, x₀)

верно при любой системе допустимых значений параметров.

Совокупность всех частных решений неравенства (1) называется общим решением этого неравенства.

Решить неравенство (1) – значит указать, при каких значениях параметров существует общее решение и каково оно.

Два неравенства

f(a, b, c, …, k, x)>j(a, b, c, …, k, x)  и        (1)

z(a, b, c, …, k, x)>y(a, b, c, …, k, x)           (2)

называются равносильными, если они имеют одинаковые общие решения при одном и том же множестве систем допустимых значений параметров.

 

2. Алгоритм решения.

1.    Находим область определения данного неравенства.

2.    Сводим неравенство к уравнению.

3.    Выражаем а как функцию от х.

4.    В системе координат хОа строим графики функций а =f (х) для тех значений х, которые входят в область определения данного неравенства.

5.    Находим множества точек, удовлетворяющих данному неравенству.

6.    Исследуем влияние параметра на результат.

·      найдём абсциссы точек пересечения графиков.

·      зададим прямую а=соnst  и будем сдвигать её от -∞ до +∞

7.    Записываем ответ.

Это всего лишь один из алгоритмов решения неравенств с параметрами, с использованием системы координат хОа. Возможны и другие методы решения, с использованием стандартной системы координат хОy. 

3. Примеры

I. Для всех допустимых значений параметра  а  решить неравенство

 

Решение.

В области определения параметра а, определённого системой неравенств

данное неравенство равносильно системе неравенств

Если , то решения исходного неравенства заполняют отрезок  .

Ответ: , .

 

II. При каких значениях параметра а имеет решение система

 

Решение.

Найдем корни трехчлена левой части неравенства  –

                             (*)

Прямые, заданные равенствами (*), разбивают координатную плоскость аОх на четыре области, в каждой из которых квадратный трехчлен

сохраняет постоянный знак. Уравнение (2) задает окружность радиуса  2  с центром в начале координат. Тогда решением исходной системы будет пересечение заштрихован

ной области с окружностью, где , а значения  и  находятся из системы

а значения  и  находятся из системы

Решая эти системы, получаем, что

Ответ:

 

III. Решить неравенство  на  в зависимости от значений параметра а.

 

Решение.

                        Находим область допустимых значений –

                        Построим график функции в системе координат хОу.

·    при  неравенство решений не имеет.

·    при  для  решение х удовлетворяет соотношению , где

 

Ответ: Решения неравенства существуют при 

, где  , причем при  решения ; при  решения  .

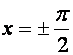IV. Решить неравенство

 

Решение.

                        Находим ОДЗ или линии разрыва (асимптоты)

 

                                        

 

                        Найдем уравнения функций, графики которых нужно построить в ПСК; для чего перейдем к равенству :

 

 

Разложим числитель на множители.

т. к.    то

Разделим обе части равенства на  при . Но  является решением : левая часть уравнения равна правой части и равна нулю при .

3. Строим в ПСК хОа  графики функций

 

и нумеруем  образовавшиеся области (оси роли не играют). Получилось девять областей.

4. Ищем, какая из областей подходит для данного неравенства, для чего берем точку из области и подставляем в неравенство.

Для наглядности составим таблицу.

 

 

5. Найдем точки пересечения графиков

6. Зададим прямую а=сonst и будем сдвигать её от  -∞ до + ∞.

Ответ.

при                                                               

при                                                               

при                                                   

при                                                           решений нет

при                                                          

Литература