Уравнения с параметрами
Страницы: 1 | 2
1. Теоретические основы решения уравнений с параметрами.
Рассмотрим уравнение
F(х, у, ..., z; α,β,..., γ) = 0 (F)
с неизвестными х, у, ..., z и с параметрами α,β, ..., γ; при всякой допустимой системе значений параметров α0,β0, ..., γ0 уравнение (F) обращается в уравнение
F(х,
у, ..., z; α0,β0, ..., γ0) =0 (F0)
с неизвестными х, у,..., z, не содержащее параметров. Уравнение (Fo) имеет некоторое вполне определенное множество (быть, может, пустое) решений.
Аналогично рассматриваются системы уравнений, содержащих параметры. Допустимыми системами значений параметров считаются системы, допустимые для каждого уравнения в отдельности.
Определение. Решить уравнение (или систему), содержащее параметры, это значит, для каждой допустимой системы значений параметров найти множество всех решений данного уравнения (системы).
Понятие эквивалентности применительно к уравнению, содержащим параметры, устанавливается следующим образом.
Определение. Два уравнения (системы)
F(х, у, ..., z; α,β, ..., γ) =0 (F),
Ф (х, у, ..., z; α,β, ..., γ) =0 (Ф)
с неизвестным х, у,..., z и с параметрами α,β, ..., γ называются эквивалентными, если для обоих уравнений (систем) множество допустимых систем значений параметров одно и то же и при всякой допустимой системе значений, параметров оба уравнения (системы уравнений) эк-вивалентны.
Итак, эквивалентные уравнения при всякой допустимой системе значений параметров имеют одно и то же множество решений.
Преобразование уравнения, изменяющее множество допустимых систем значений параметров, приводит к уравнению, не эквивалентному данному уравнению.
Предположим, что каждое из неизвестных, содержащихся в уравнении
F(x, у,z; α,β, ..., γ)=0 (F)
задано в виде некоторой функции от параметров:
х = х(α,β, ..., γ);
у = у(α,β, ..., γ);….
Говорят, что система функций (Х), заданных совместно, удовлетворяет уравнению (F), если при подстановке этих функций вместо неизвестных х, у,..., z в уравнение (F) левая его часть обращается в нуль тождественно при всех допустимых значениях параметров:
F (x(α,β, ..., γ), y(α,β, ..., γ),…,z (α,β, ..., γ) ≡ 0.
При всякой допустимой системе численных значений параметров α = α0,β=β0, ..., γ= γ0 соответствующие значения функций (Х) образуют решение уравнения
F(х, у, ..., z; α0,β0, ..., γ0) =0
2. Основные виды уравнений с параметрами
Линейные и квадратные уравнения
1. Если а ≠ 0 , то при любой паре параметров а и b оно имеет единственное решение х =
![]() .
.
2. Если а = 0, то уравнение принимает вид: 0 х = b. В этом случае значение b = 0 является особым значением параметра b.
2.1. При b ≠ 0 уравнение решений не имеет.
2.2.
При b = 0 уравнение примет вид : 0 х = 0. Решением данного уравнения является любое действительное число.
П р и м е р . Решим уравнение
2а(а — 2) х=а — 2. (2)
Р е ш е н и е. Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в 0. Такими значениями являются а=0 и а=2. При этих значениях а невозможно деление обеих частей уравнения на коэффициент при х. В то же время при значениях параметра а≠0, а≠2 это деление возможно. Таким образом, целесообразно множество всех действительных значений параметра разбить на подмножества
A1={0}, А2={2} и Аз= {а≠0, а≠2}
и решить уравнение (2) на каждом из этих подмножеств, т. е. решить уравнение (2) как семейство уравнений, получающихся из него при следующих значениях параметра:
1) а=0 ; 2) а=2 ; 3) а≠0, а≠2
Рассмотрим эти случаи.
1) При а=0 уравнение (2) принимает вид 0 х= — 2. Это уравнение не имеет корней.
2) При а=2 уравнение (2) принимает вид 0 х=0. Корнем этого уравнения является любое действительное число.
3) При а≠0, а≠2 из уравнения (2) получаем, х=
![]()
откуда х=
![]() .
.
0 т в е т: 1) если а=0, то корней нет; 2) если а=2, то х — любое действительное число; 3) если а≠0, а≠2 , то х=
![]()
П р и м е р . Решим уравнение
(а — 1) х2+2 (2а+1) х+(4а+3) =0; (3)
Р е ш е н и е. В данном случае контрольным является значение a=1. Дело в том, что при a=1 уравнение (3) является линейным, а при а≠ 1 оно квадратное (в этом и состоит качественное изменение уравнения). Значит, целесообразно рассмотреть уравнение (3) как семейство уравнений, получающихся из него при следующих значениях параметра: 1) а=l; 2) а≠1.
Рассмотрим эти случаи.
1) При a=1 уравнение (3) примет вид бх+7=0. Из этого
уравнения находим х= -
![]() .
.
2) Из множества значений параметра а≠ 1 выделим те значения, при которых дискриминант уравнения (3) обращается в 0.
Дело в том, что если дискриминант D=0 при а=ао, то при переходе значения D через точку ао дискриминант может изменить знак (например, при а<ао D< 0, а при а>ао D>0). Вместе с этим при переходе через точку ао меняется и число действительных корней квадратного уравнения (в нашем примере при а<ао корней нет, так как D< 0, а при а>ао D>0 уравнение имеет два корня). Значит, можно говорить о качественном изменении уравнения. Поэтому значения параметра, при которых обращается в 0 дискриминант квадратного уравнения, также относят к контрольным значениям.
Составим дискриминант уравнения (3):
![]() =(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем
=(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем
![]() = 5а+4.
= 5а+4.
Из уравнения
![]() =0 находим а=
=0 находим а=
![]() — второе контрольное значение параметра а. При
— второе контрольное значение параметра а. При
![]() этом если а <
этом если а <
![]() , то D <0; если a≥
, то D <0; если a≥
![]() , , то D≥0.
, , то D≥0.
a ≠ 1
Таким образом, осталось решить уравнение (3) в случае, когда а<
![]() и в случае, когда { a≥
и в случае, когда { a≥
![]() , a ≠ 1 }.
, a ≠ 1 }.
Если а<
![]() , то уравнение (3) не имеет действительных корней; если же
, то уравнение (3) не имеет действительных корней; если же
{ a≥
![]() , a ≠ 1 }, то находим
, a ≠ 1 }, то находим
![]()
Ответ: 1) если а<
![]() , то корней нет ; 2) если а= 1, то х = -
, то корней нет ; 2) если а= 1, то х = -
![]() ;
;
![]() 3) a ≥
3) a ≥
![]() , то
, то
![]() , a ≠ 1
, a ≠ 1
Дробно-рациональные уравнения с параметрами, сводящиеся к линейным.
П р и м ер . Решим уравнение
![]() (4)
(4)
Р е ш е н и е. Значение а=0 является контрольным. При a=0 уравнение (4) теряет смысл и, следовательно, не имеет корней. Если а≠0, то после преобразований уравнение (4) примет вид:
х2+2 (1 — а) х +а2 — 2а — 3=0. (5)
Найдем дискриминант уравнения (5)
![]() = (1 — a)2 — (a2 — 2а — 3) = 4.
= (1 — a)2 — (a2 — 2а — 3) = 4.
Находим корни уравнения (5):
х1 =а + 1, х2 = а — 3.
При переходе от уравнения (4) к уравнению (5) расширилась
область определения уравнения (4), что могло привести к появлению посторонних корней. Поэтому необходима проверка.
П р о в е р к а. Исключим из найденных значений х такие, при которых х1+1=0, х1+2=0, х2+1=0, х2+2=0.
Если х1+1=0, т. е. (а+1)+1=0, то а= — 2. Таким образом, при а= — 2 х1 — посторонний корень уравнения (4).
Если х1+2=0, т. е. (а+1)+2=0, то а= — 3. Таким образом, при а= — 3 x1 — посторонний корень уравнения (4).
Если х2+1 =0, т. е. (а — 3)+1=0, то а=2. Таким образом, при а=2 х2 — посторонний корень уравнения (4)'.
Если х2+2=0, т. е. (а — 3)+2=0, то а=1. Таким образом, при а= 1 х2 — посторонний корень уравнения (4).
Для облегчения выписывания ответа сведем полученные результаты на рисунке .
при a= — 2 х= — 2 — 3= — 5; при a=1 х= 1+1=2; при a=2 х=2+1=3.
Итак, можно записать
От в ет: 1) если a= — 3, то х= — 6; 2) если a= — 2, то х= — 5; 3) если a=0, то корней нет; 4) если a= l, то х=2; 5) если а=2, то х=3;
6) если а≠ -3 ;
а≠ -2 ;
а≠ 0 ; то х1 = а + 1,
а≠ 1 ; х2 = а – 3.
а≠ 2,
Иррациональные уравнения с параметрами.
Существует несколько способов решения иррациональных уравнений с параметрами. Познакомимся с ними, разобрав следующий пример.
П р и м ер . Решить уравнение х -
![]() = 1. (6)
= 1. (6)
Решение:
Возведем в квадрат обе части иррационального уравнения с последующей проверкой полученных решений.
Перепишем исходное уравнение в виде:
![]() = х – 1 (7)
= х – 1 (7)
При возведении в квадрат обеих частей исходного уравнения и проведения тождественных преобразований получим:
2 х2 – 2х + (1 - а) = 0, D = 2а – 1.
Особое значение : а = 0,5. Отсюда :
1)
при а > 0,5 х1,2 = 0,5 ( 1 ±
![]() );
);
2) при а = 0,5 х = 0,5 ;
3) при а <0,5 уравнение не имеет решений.
Проверка:
1) при подстановке х = 0,5 в уравнение (7), равносильное исходному, получим неверное равенство. Значит, х = 0,5 не является решением (7) и уравнения (6).
2)
при подстановке х1 = 0,5 ( 1 ±
![]() ) в (7) получим:
) в (7) получим:
-0,5 ( 1 +
![]() ) =
) =
![]() – ( 0,5 ( 1 -
– ( 0,5 ( 1 -
![]() ))2
))2
Так как левая часть равенства отрицательна, то х1 не удовлетворяет исходному уравнению.
3) Подставим х2 в уравнение (7):
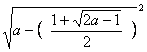 =
=
![]()
Проведя равносильные преобразования, получим:
Если
![]() , то можно возвести полученное равенство в квадрат:
, то можно возвести полученное равенство в квадрат:
![]()
Имеем истинное равенство при условии, что
![]()
Это условие выполняется, если а ≥1. Так как равенство истинно при а ≥1, а х2 может быть корнем уравнения (6) при а > 0,5, следовательно, х2 – корень уравнения при а ≥1.
Тригонометрические уравнения.
Большинство тригонометрических уравнений с параметрами сводится к решению простейших тригонометрических уравнений трех типов. При решении таких уравнений необходимо учитывать ограниченность тригонометрических функций у = sin x и y = cos x. Рассмотрим примеры.
Пример . Решить уравнение: cos
![]() =2а.
=2а.
Решение: Так как Е(соs t)=[-1; 1], то имеем два случая.
1. При |a| > 0,5 уравнение не имеет решений.
2. При |a| ≤0,5 имеем:
а)
![]() =arccos2a+2πn. Так как уравнение имеет решение, если arccos2а+2πn≥0, то n может принимать значения n=0, 1, 2, 3,.... Решением уравнения является х = 1+(2πn+аrссоs2а)2
=arccos2a+2πn. Так как уравнение имеет решение, если arccos2а+2πn≥0, то n может принимать значения n=0, 1, 2, 3,.... Решением уравнения является х = 1+(2πn+аrссоs2а)2
б)
![]() =-аrссоs2а+πn. Так как уравнение имеет решение при условии, что -аrссоs2а+2πn>0, то n=1, 2, 3,..., и решение уравнения. х=1+(2πn-arccos2a)2 .
=-аrссоs2а+πn. Так как уравнение имеет решение при условии, что -аrссоs2а+2πn>0, то n=1, 2, 3,..., и решение уравнения. х=1+(2πn-arccos2a)2 .
Ответ: если |a| > 0,5, решений нет;
если |a| ≤0,5 , х = 1+(2πn+аrссоs2а)2при n = 0, 1, 2,... и х=1+(2πn-arccos2a)2 при n
![]() N.
N.
Пример . Решить уравнение: tg ax2 =
![]()
Решение:.
ах2 =
![]() +πn, n
+πn, n
![]() Z
Z
Если коэффициент при неизвестном зависит от параметра, то появляется особое значение параметра. В данном случае:
1. Если а=0, то уравнение не имеет решений.
2. Если а
![]() 0, то х2 =
0, то х2 =
![]() , n
, n
![]() Z
Z
Уравнение имеет решение, если
![]() ≥
0. Выясним, при каких значениях n
≥
0. Выясним, при каких значениях n
и а выполняется это условие:
![]() ≥
0
≥
0
![]()
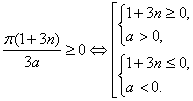
откуда n ≥
![]() и а > 0 или n ≤
и а > 0 или n ≤
![]() и а < 0.
и а < 0.
Итак, уравнение имеет решение х = ±
![]() , если
, если
1) а > 0 и n = 1,2,3,… или
2) а < 0 и n
![]() Z.
Z.
Ответ: при а = 0 решений нет;
при а > 0 и n = 1,2,3,… или а < 0 и n
![]() Z х = ±
Z х = ±
![]() .
.
Пример. Решите уравнение: а sin bx = 1
Решение: Особое значение параметра а : а = 0.
1. При а = 0 решений нет.
2.
При а
![]() 0 sin bx =
0 sin bx =
![]() . Имеем 2 случая:
. Имеем 2 случая:
2.1. Если
![]() > 1, то решений нет.
> 1, то решений нет.
2.2. Если
![]() ≤ 1, то особое значение b = 0:
≤ 1, то особое значение b = 0:
2.2.1. Если b = 0, то решений нет.
2.2.2. Если b
![]() 0, то х =
0, то х =
![]()
Ответ: при а = 0 или
![]() > 1 и а
> 1 и а
![]() 0 или а
0 или а
![]() 0 b = 0 решений нет;
0 b = 0 решений нет;
при а
![]() 0 и
0 и
![]() ≤ 1 и b
≤ 1 и b
![]() 0 х =
0 х =
![]()
Страницы: 1 | 2
